What is a Binomial Tree and its Importance in Computer Programming?

A binomial tree is an order with one node built from two other binomial trees, making it either one or the other. It is employed in asset valuation. Several binomial trees converge to form binomial heaps with a variety of values. It is an important and practical instrument for pricing. It is straightforward, which is both a benefit and a drawback. 

The binomial tree is simple to construct and mechanically represent, but the values of the underlying asset are where the main issues arise. The investment can be worth any number of values inside a specific range. Hence the binomial tree model's restriction that it can only be worth two conceivable values is frequently unrealistic. The investor can analyse when a value and its option can be exercised using the binomial tree.

Only when the choice has a positive value can it be used to determine a matter of high likelihood. Different approaches can be employed in value, such as the faster black Scholes model. However, for assessing the importance of the numbers, the binomial tree is the most trustworthy and credible option.

Role Of Binomial tree in programming

The significance of the binomial tree is not only based on stock and pricing but also comes in handy in programming, data structure, and other sectors.

Programs for analysing or preparing for playing traditional board games in tournaments can be found in binomial software. The user interface, opening book, historical archive, riddles, and endgame database are all included in each programme as a whole. Our software doesn't need to be activated or connected to the internet and is compatible with the most popular operating systems, including Windows, Mac, and Linux. There is only the checkers version available at the moment now.

A method for valuing options was created in 1979 and is known as the binomial option pricing model.

The iterative process used by the binomial option pricing model enables the specification of nodes, or points in time, between the valuation date and the option's expiration date.

Properties of the binomial tree

Few characteristics define a binomial tree. As follows:

• Made up of 2k nodes.
• It has K-level depth.
• At the depth, there are kainic nodes.
• Every root has a degree of k.
• According to k-1, k-2, and so forth, the order is from left to right.
• The lower node is multiplied, moved to the upper side, and the presiding high code is multiplied by the lower one to determine each node's value.
• The calculation's fundamental requirement is that it provides the same outcome.
• The asset price starts with the node, which indicates the starting price and separates the two nodes into one with the likely cost of the underlying item and the other in the future point. This is another crucial characteristic. Depending on the price at the time of the asset's genesis, its value may increase or decrease.
• The binomial tree can be used to value calls and set up options using the price that is most likely to correspond to the underlying movements of the asset.

A binomial tree can be used to examine values while undertaking and evaluating these qualities.

How to make a binomial tree?

Excel sheets and conventional methods can be used to create binomial trees easily, and it is the most effective method for visualising the model. The option payoff and probability at various modes are shown with the use of a binomial way. The node provides a timeline for the oaths of the asset's price that it underlines. It can also be viewed as a standard one-period call option. The following is one method:

Binomial tree formula

According to the assignment help experts- Binomial tree calculations can be made simpler using an excel spreadsheet. It is adaptable because it may consider the shifting conditions in various ways, making it a viable method for assessing early exit alternatives. With regard to the Black Scholes model, they both produce comparable evaluation outcomes when the viability is a binary price choice.

However, several restrictions still make it difficult to estimate future pricing accurately. It gets more laborious when there is a chance to predict the anticipated payoffs at the end of each period node. Numerous binomial trees combine to form a binomial heap, which is then used to price and analyse a value up to its maximum potential. The computation can be time-consuming but is far more reliable if it is based on formulas as well as an excel spreadsheet.

Structure

A binary tree When k is specified as the order of the binomial tree, then Bk is an ordered tree that is defined recursively

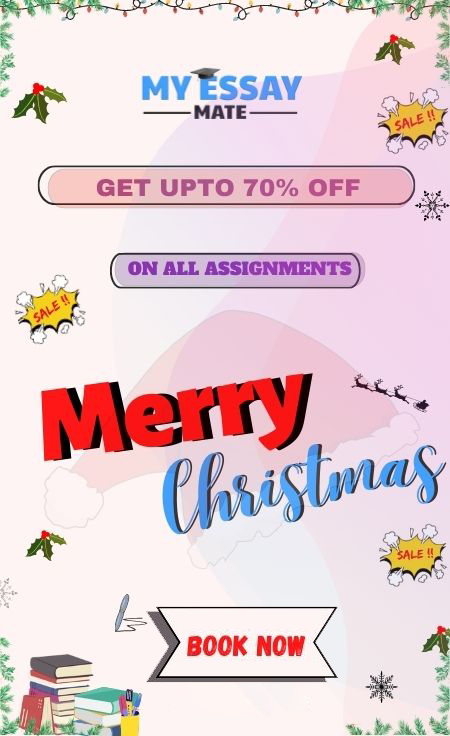
There is just one node when the binomial tree is written as B0.

Bk, in its most basic form, is made up of two linked binomial trees, Bk-1 and Bk-1, where one tree becomes the left subtree of the other.

We can understand it with the example given below.

There would be only one node in the tree if B0, where k is 0.

If B1, and k are 1, then. As a result, there would be two B0 binomial trees, each of which is the left subtree of the other.

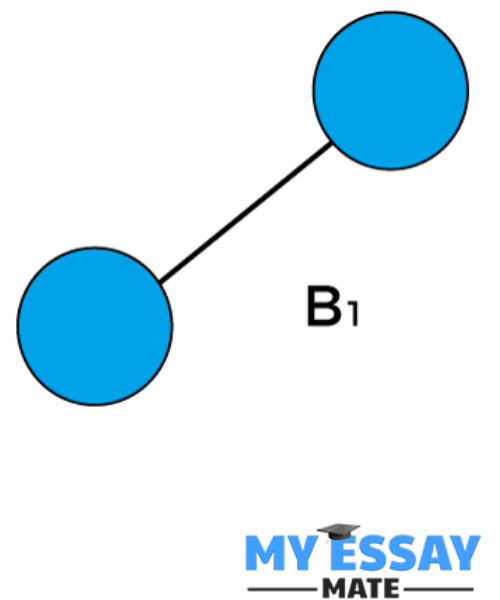
If B2, and k are 2, then. As a result, there would be two B1 binomial trees, where one of them is the left subtree of the other.

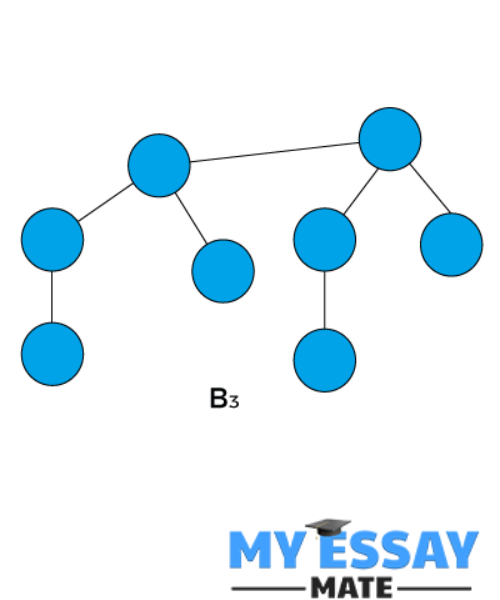
If B3, and k are 3, then. As a result, there would be two B2 binomial trees, each of which is the left subtree of the other.

Find it difficult to understand? Do not worry; check with our mentors at Online Assignment Expert to ensure an in-depth understanding of your topic and a perfect programming assignment help!

Binomial Trees Examples in simple words

As an illustration, consider a specific stock with the current year's value of $. Within the predetermined expiration window, the ATM option's strike price is $50. Two traders, John and Michael, predict that the price will rise to $60 or fall to $40 in a year. They could disagree on the possibility that prices would grow or lose, but they agreed on the expected level for a specific period within a year. John believes it to be 60, which would be 60%, but Michael believes it to be 40, or 40%. This is how the binomial works; it would be used to predict the cost of the call option.

Samples

Need programming assignment help? Get in touch with Online Assignment Expert!

On that note, we hope you like this blog, and if you did, you will surely want to connect with our mentors who put their 100% energy and knowledge into making your study life more accessible.

As you know, there are multiple queries for your binomial tree, and you need someone to tell you how to do the assignments. So, the good news is that we have great programming assignment help experts at Online Assignment Expert who help you become better writers. Since binomial trees have multiple applications in different sectors, it is essential to know that you have knowledge about each one of them, especially when it comes to engineering. Here are some practical ways how help our students to learn and grow!

• Our professionals consistently deliver original work. In addition, the information for the subject is carefully chosen and utilised for the project. To write the assignment most efficiently, research is crucial.
• To guarantee our work's originality, we always include a Turnitin report, and this is specifically for our work.
• The first thing our programming assignment assistance professionals do is read over the assignment's criteria and look over any questions. Clients are alerted in case of a query and asked to supply the necessary information for the assignment. In order to create a segment in the assignment, the word count is now verified. It is also stated that the work must be finished in accordance with university regulations.
• Our specialists are skilled at completing assignments by the deadline and to a high-quality standard. In addition, customers can specify any other needs they may have on the portal. If a client has a question, they can post it on the site, and it will be answered as quickly as feasible.
• We always attempt to ensure that our solutions and efforts are in line with the assignment's specifications.
• Since all programming assignments are hard to comprehend, we also ensure to provide samples as the first draft where you can understand the expectation of your professors and prepare a new study out of it. All you need to do is request the draft by getting in touch with experts and telling them about the topic.

So, give yourself the treat of having the best programming assignment help at the lowest price. Today!